Numerical Solution Technique
Horizontal Discretization
In the horizontal, the ROMS governing equations are discretized over a boundary-fitted, orthogonal curvilinear coordinates (ξ, η) grid. The general formulation of the curvilinear coordinates system allows Cartesian, polar and spherical coordinates applications. The transformation of any of these coordinates to ROMS (ξ, η) grid is specified in the metric terms (pm, pn).
The state variables are staggered using an Arakawa C-grid. As illustrated below, the free-surface (zeta), density (ρ), and active/passive tracers (t) are located at the center of the cell whereas the horizontal velocity (u, v) are located at the (west/east, south/north) edges of the cell. That is, the density is evaluated between points where the currents are evaluated.
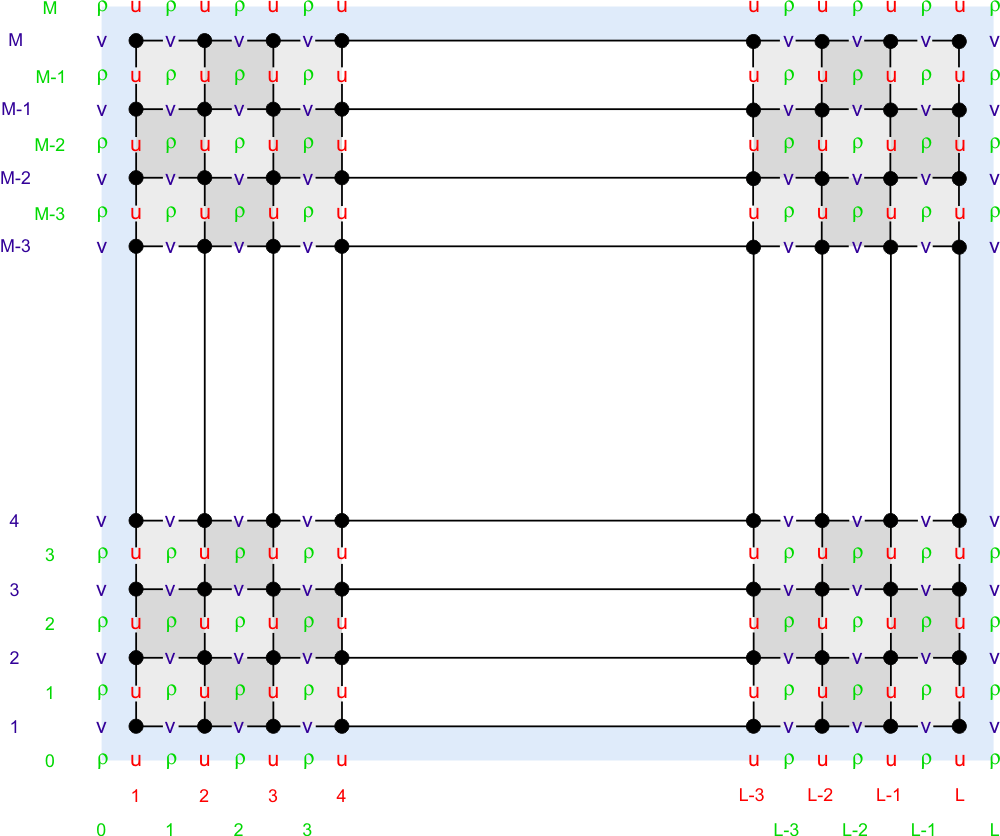
In ROMS all the state arrays are dimensioned the same to facilitate parallelization.
Coastal boundaries can also be specified as a finite-discretized grid via land/sea masking arrays (rmask, umask, and vmask).
Vertical Discretization
The ROMS governing equations are discretized over variable topography using a stretched, terrain-following, vertical coordinate. As a result, each grid cell may have different level thickness (Hz) and volume. The model state variables are vertically staggered so that horizontal momentum (u, v), (ρ), and active/passive tracers (t) are located at the center of the grid cell. The vertical velocity (ω, w) and vertical mixing variables (Akt, Akv, etc) are located at the bottom and top faces of cell. See diagram below.
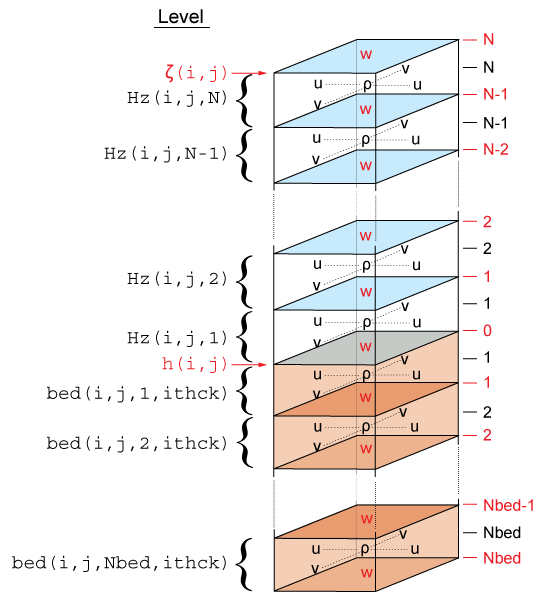
The total thickness of the water column is ζ(i,j)+h(i,j)
. The bathymetry (h) is usually time invariant whereas the free-surface (ζ) evolves in time. However, in sediment applications h changes with time when SED_MORPH is activated. At input and output, the bathymetry is always a positive quantity. However, the depths z_r(i,j,k) and z_w(i,j,k) of every grid cell are negative quantities in ROMS.