I4DVAR ANA SENSITIVITY

I4DVAR_ANA_SENSITIVITY (Formerly IS4DVAR_SENSITIVITY)

Option to activate the observation impact and sensitivity driver which quantifies the impact that each observation has on the 4DVAR data assimilation system. By measuring the sensitivity of the data assimilation system to each observation, we can determine the degree to which each observation contributes to the uncertainty in the circulation estimate. This analysis can help us to determine the type of measurements that need to be made, where to observe, and when.

required = ADJOINT, NONLINEAR, TANGENT

related = I4DVAR, LANCZOS

routine = obs_sen_i4dvar_analysis.h

Mathematical Formulation

The mathematical development presented here closely parallels that of Zhu and Gelaro (2008). The sensitivity of any functional, $\mathcal{J}$, of the analysis ${\mathrm{\Psi }}_{\mathbf{a}}$ or forecast ${\mathrm{\Psi }}_{\mathbf{f}}$ can be efficiently computed using the adjoint model which yields information about the gradients of $\mathcal{J}({\mathrm{\Psi }}_{\mathbf{a}})$ and $\mathcal{J}({\mathrm{\Psi }}_{\mathbf{f}})$. We can extent the concept of the adjoint sensitivity to compute the sensitivity of the IS4DVAR cost function, $J$, in (1) and any other function $\mathcal{J}$ of the forecast ${\mathrm{\Psi }}_{\mathbf{f}}$ to the observations, $\mathbf{y}$.

In IS4DVAR, we define a quadratic cost function:

$$J(\psi )=\frac{1}{2}{\psi }^T{\mathbf{B}}^{-1}\psi +\frac{1}{2}(\mathbf{G}\psi -\mathbf{d}{)}^T{\mathbf{O}}^{-1}(\mathbf{G}\psi -\mathbf{d})$$

(1)

where $\psi$ is the ocean state vector ($\zeta$, $u$, $v$, $T$, $S$,$\dots$) with $\psi \equiv \psi (t_0)$, $\mathbf{O}$ is the observation error and error of representativeness covariance matrix, $\mathbf{B}$ represents the background error covariance matrix, $\mathbf{d}$ is the innovation vector that represents the difference between the nonlinear background solution (${\mathrm{\Psi }}_{\mathbf{b}}$) and the observations, ${\mathbf{d}}_i={\mathbf{y}}_i-{\mathbf{H}}_i({\mathrm{\Psi }}_{\mathbf{b}}(t_i))$. Here, ${\mathbf{H}}_i$ is an operator that samples the nonlinear model at the observation location, $\mathbf{G}={\mathbf{H}}_i^{\prime }\mathbf{R}(t_0,t_i)$, ${\mathbf{H}}_i^{\prime }$ is the linearization of ${\mathbf{H}}_i$, and the operator $\mathbf{R}$ is referred as the tangent linear model propagator.

At the minimum of (1), the cost function gradient $\partial J/\partial \psi$ vanishes and:

$$\psi \equiv {\psi }_a=({\mathbf{B}}^{-1}+{\mathbf{G}}^T{\mathbf{O}}^{-1}\mathbf{G}{)}^{-1}{\mathbf{G}}^T{\mathbf{O}}^{-1}\mathbf{d},$$

(2)

where ${\psi }_a$ is referred to as the analysis increment, the desired solution of the incremental data assimilation procedure.

The IS4DVAR analysis can be written in the more traditional form as ${\mathrm{\Psi }}_{\mathbf{a}}={\mathrm{\Psi }}_{\mathbf{b}}+\mathbf{K}\mathbf{d}$ ( Daley, 1991), where ${\psi }_a=\mathbf{K}\mathbf{d}$, the Kalman gain matrix $\mathbf{K}={\mathcal{H}}^{-1}{\mathbf{G}}^T{\mathbf{O}}^{-1}$, and $\mathcal{H}={\partial }^{2}J/\partial {\psi }^2={\mathbf{B}}^{-1}{\mathbf{G}}^T{\mathbf{O}}^{-1}\mathbf{G}$ is the Hessian matrix. The entire IS4DVAR procedure is therefore neatly embodied in $\mathbf{K}$. At the cost function minimum, (1) can be written as $J=\frac{1}{2}{\mathbf{d}}^T(\mathbf{I}-{\mathbf{K}}^T{\mathbf{G}}^T){\mathbf{O}}^{-1}\mathbf{d}$ which yields the sensitivity of the IS4DVAR cost function to the observations.

In the current IS4DVAR/LANCZOS data assimilation algorithm, the cost function minimum of (1) is identified using the Lanczos method (Golub and Van Loan, 1989), in which case:

$${\mathrm{\Psi }}_{\mathbf{a}}={\mathrm{\Psi }}_{\mathbf{b}}-{\mathbf{Q}}_k{\mathbf{T}}_k^{-1}{\mathbf{Q}}_k^T{\mathbf{G}}^T{\mathbf{O}}^{-1}\mathbf{d}$$

(3)

where ${\mathbf{Q}}_k=({\mathbf{q}}_i)$ is the matrix of $k$ orthogonal Lanczos vectors, and ${\mathbf{T}}_k$ is a known tridiagonal matrix. Each of the $k-$iterations of IS4DVAR employed in finding the minimum of $J$ yields one column ${\mathbf{q}}_i$ of ${\mathbf{Q}}_k$. From (3) we can identify the Kalman gain matrix as $\mathbf{K}=-{\mathbf{Q}}_k{\mathbf{T}}_k^{-1}{\mathbf{Q}}_k^T{\mathbf{G}}^T{\mathbf{O}}^{-1}$ in which case ${\mathbf{K}}^T=-{\mathbf{O}}^{-1}\mathbf{G}{\mathbf{Q}}_k{\mathbf{T}}_k^{-1}{\mathbf{Q}}_k^T$ represents the adjoint of the entire IS4DVAR system. The action of ${\mathbf{K}}^T$ on the vector ${\mathbf{G}}^T{\mathbf{O}}^{-1}\mathbf{d}$ in (3) can be readily computed since the Lanczos vectors ${\mathbf{q}}_i$ and the matrix ${\mathbf{T}}_k$ are available at the end of each IS4DVAR assimilation cycle.

Therefore, the basic observation sensitivity algorithm is as follows:

1. Force the adjoint model with ${\mathbf{O}}^{-1}\mathbf{d}$ to yield ${\psi }^{†}={\mathbf{G}}^T{\mathbf{O}}^{-1}\mathbf{d}\propto {\mathbf{q}}_i$.
2. Operate on ${\psi }^{†}(t_0)$ with ${\mathbf{Q}}_k{\mathbf{T}}_k^{-1}{\mathbf{Q}}_k^T$ which is equivalent to a rank$-k$ approximation of the Hessian matrix.
3. Integrate the results of step (ii) forward in time using the tangent linear model and save the solution ${\mathbf{H}}^{\prime }\psi (t_i)$. That is, the solution at observation locations.
4. Multiply ${\mathbf{H}}^{\prime }\psi (t_i)$ by $-{\mathbf{O}}^{-1}$ to yield $\partial J/\partial \mathbf{y}$.

Consider now a forecast ${\mathrm{\Psi }}_{\mathbf{f}}(t)$ for the interval $t=[t_0+\tau ,t_0+\tau +t_f]$ initialized from ${\mathrm{\Psi }}_{\mathbf{a}}(t_0+\tau )$ obtained from an assimilation cycle over the interval $t=[t_0,t_0+\tau ]$, where $t_f$ is the forecast lead time. In addition, consider $\mathcal{J}({\mathrm{\Psi }}_{\mathbf{f}}(t))$ that depends on the forecast ${\mathrm{\Psi }}_{\mathbf{f}}(t)$, and which characterizes some future aspect of the forecast circulation. According to the chain rule, the sensitivity $\partial \mathcal{J}/\partial \mathbf{y}$ of $\mathcal{J}$ to the observations $\mathbf{y}$ collected during the assimilation cycle $t=[t_0,t_0+\tau ]$ is given by:

$$\frac{\partial \mathcal{J}}{\partial \mathbf{y}}=\frac{\partial {\mathrm{\Psi }}_{\mathbf{a}}}{\partial \mathbf{y}}\frac{\partial {\mathrm{\Psi }}_{\mathbf{f}}}{\partial {\mathrm{\Psi }}_{\mathbf{a}}}\frac{\partial \mathcal{J}}{\partial {\mathrm{\Psi }}_{\mathbf{f}}}=-{\mathbf{O}}^{-1}\mathbf{H}\mathbf{R}{\mathbf{Q}}_k{\mathbf{T}}_k^{-1}{\mathbf{Q}}_k^T{\mathbf{R}}^T\frac{\partial \mathcal{J}}{\partial {\mathrm{\Psi }}_{\mathbf{f}}}$$

(4)

which again can be readily evaluated using the adjoint model denoted by ${\mathbf{R}}^T(t,t_0+\tau )$ and the adjoint of IS4DVAR, ${\mathbf{K}}^T$.

Technical Description

This ROMS driver can be used to evaluate the impact of each observation on the IS4DVAR data assimilation algorithm by measuring their sensitivity over a specified circulation functional index, $\mathcal{J}$. This algorithm is an extension of the adjoint sensitivity driver, AD_SENSITIVITY. As mentioned above, this algorithm is equivalent to taking the adjoint of the IS4DVAR algorithm.

The following steps are carried out in obs_sen_is4dvar.h:

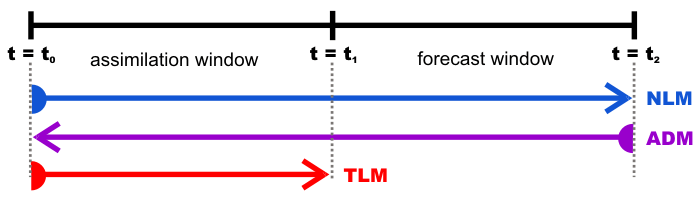
1. We begin by running the incremental strong constraint 4DVar data assimilation algorithm (IS4DVAR) with the Lanczos conjugate gradient minimization algorithm (LANCZOS) using $k$ inner-loops ($\text{Ninner}=k$) and a single outer-loop ($\text{Nouter}=1$) for the period $t=[t_0,t_1]$. We will denote by ${\mathrm{\Psi }}_{\mathbf{b}}(t_0)$ the background initial condition, and the observations vector by $\mathbf{y}$. The resulting Lanczos vectors that we save in the adjoint NetCDF file will be denoted by ${\mathbf{q}}_i$, where $i=1,2,\dots ,k$.
2. Next we run the nonlinear model for the combined assimilation plus forecast period $t=[t_0,t_2]$, where $t_2\ge t_1$. This represents the final sweep of the nonlinear model for the period $t=[t_0,t_1]$ after exiting the inner-loop in the IS4DVAR plus the forecast period $t=[t_1,t-2]$. The initial condition for the nonlinear mode at $t=t_0$ is ${\mathrm{\Psi }}_{\mathbf{b}}(t_0)$ and not the new estimated initial conditions, $\mathrm{\Psi }(t_0)={\mathrm{\Psi }}_{\mathbf{b}}(t_0)+\psi (t_0)$. We save the basic state trajectory, ${\mathrm{\Psi }}_{\mathbf{b}}(t)$, of this nonlinear model run for use in the adjoint sensitivity calculation next, and for use in the tangent linear model run later in step (vii). Depending on time for which the sensitivity functional $\mathcal{J}(t)$ is defined, this will dictate $t_2$. For example, if $\mathcal{J}(t)$ is a functional defined during the forecast interval $t_1<t<t_2$, then $t_2>t_1$ for this run of the nonlinear model. However, if $\mathcal{J}(t)$ is defined during the assimilation interval $t_0<t<t_1$, then $t_2=t_1$. That is, the definition of $t_2$ should be flexible depending on the choice of $\mathcal{J}$.
3. The next step involves an adjoint sensitivity calculation for the combined assimilation plus forecast period $t=[t_2,t_0]$. The basic state trajectory for this calculation will be that from the nonlinear model run in step (ii).
4. After running the regular adjoint sensitivity calculation in (iii), we will have a full 3D-adjoint state vector at time $t=t_0$. Let's call this vector ${\psi }^{†}(t_0)$. The next thing we want to do is to compute the dot-product of ${\psi }^{†}(t_0)$ with each of the Lanczos vectors from the previous IS4DVAR run. So if we ran IS4DVAR with $k$ inner-loops, we will have $k-$Lanczos vectors which we denote as ${\mathbf{q}}_i$ where $i=1,2,\dots ,k$. So we will compute $a_i={\psi }^T{\mathbf{q}}_i$ where ${\psi }^T$ is the transpose of the vector ${\psi }^{†}(t_0)$, and $a_i$ for $i=1,2,\dots ,k$ are scalars, so there will be $k$ of them.
5. The next step is to invert the tridiagonal matrix associated with the Lanczos vectors. Let's denote this matrix as $\mathbf{T}$. So what we want to solve $\mathbf{T}\mathbf{b}=\mathbf{a}$, where $\mathbf{a}$ is the $k\times 1$ vector of scalars $a_i$ from step (iv), and $\mathbf{b}$ is the $k\times 1$ vector that we want to find. So we solve for $b$ by using a tridiagonal solver.
6. The next step is to compute a weighted sum of the Lanczos vectors. Let's call this $\mathbf{z}$, where $\mathbf{z}={\sum }_i(b_i{\mathbf{q}}_i)$ for $i=1,2,\dots ,k$. The $b_i$ are obtained from solving the tridiagonal equation in (v), and the ${\mathbf{q}}_i$ are the Lanczos vectors. The vector $z$ is a full-state vector and be used as an initial condition for the tangent linear model in step (vii).
7. Finally, we run the tangent linear model from $t=[t_0,t_1]$ using $\mathbf{z}$ from (vi) as the initial conditions. During this run of the tangent linear model, we need to read and process the observations $\mathbf{y}$ that we used in the IS4DVAR of step 1 and write the solution at the observation points and times to the MODname NetCDF file. The values that we write into this MODname are actually the values multiplied by error covariance $-{\mathbf{O}}^{-1}$ assigned to each observation during the IS4DVAR in step (i).