SHOREFACE CASE

Shore Face Planar Beach Test Case

This test establishes a simple case of spectral waves obliquely approaching a plane beach and is described in detail in:

Haas and Warner (2009). Comparing a quasi-3D to a full 3D nearshore circulation model: SHORECIRC and ROMS, Ocean Modelling, 26, 91-103.

The case consists of spectral waves approaching a mild sloping (1/80) plane beach with an oblique angle of incidence. The wave forcing is obtained by first running SWAN separately by specifying a JONSWAP spectrum for 2 m offshore wave height with a peak period of 10 s at an angle of 10 degrees for the incoming wave field. SWAN was configured to use 90 directional bins and 30 frequency bins between 0.04 and 0.5 Hz.

The output from SWAN was made into the ROMS forcing file: Data/ROMS/Forcing/swan_shoreface_angle_forc.nc

The circulation model computes the radiation stress forcing based on the SWAN wave output. For this application there is not a feedback of the currents to the wave model. Also we neglect the contribution from the roller model. The circulation model uses a quadratic bottom stress formulation using the depth average currents.

Results are shown after the model reaches steady state.

Figure 1: Plane beach test case results showing cross-shore variation of: (a) significant wave height (dashed) and bathymetry (solid); (b) wave setup; (c) depth-integrated cross shore currents; and (d) depth-integrated longshore currents. SHORECIRC results are solid lines, ROMS results are dashed lines (for panels b, c, and d).

Figure 1: Plane beach test case results comparing cross-shore variations of the vertical profiles of currents of: (top) cross-shore velocities; and (bottom) longshore velocities. SHORECIRC results are solid lines, ROMS results are dashed lines.

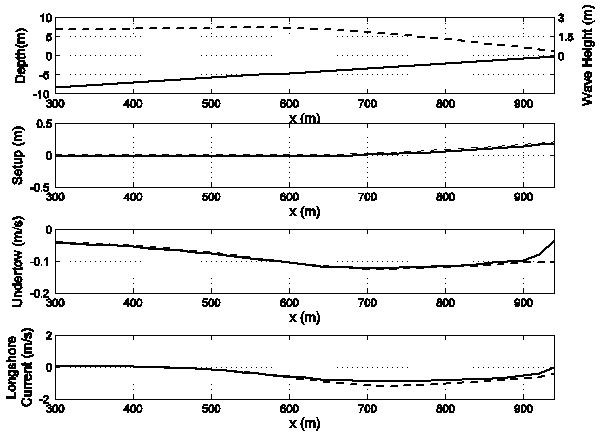
The cross-shore profiles of water depth and SWAN computed wave height are shown in Fig. 1a. The waves shoal as they enter the domain, although this is somewhat counteracted by dissipation due to bottom stress making the shoaling difficult to visualize from the wave heights in Fig. 1a. The waves begin to decrease near x = 600 m due to wave breaking dissipation. The wave fields computed from SWAN are used in each circulation model to compute the radiation stress forcing. The depth-averaged forcing as computed by each circulation model is identical, and is also identical to the forcing as computed from SWAN (not shown). Because the depth average forcing is the same, the resulting wave setup (Fig. 1b) is very similar for the two models. Similarly the depth averaged undertow and longshore currents (Fig. 1c and d) match for the two models, except near the shoreline. The differences near the shoreline are due to different treatment of the flow at the shoreline by the models. SC imposes a zero velocity shoreline condition while ROMS has a free slip shoreline condition. Overall, it is clear that with the same depth averaged forcing, and using the same bottom stress formulation, the quasi-3D and fully 3D models give very similar results for the depth averaged flow features. Therefore the redistribution of longshore momentum in the cross-shore direction due to the turbulence and vertical variation of the currents is similar for the two models.

However, the depth varying radiation stress components computed in each circulation model are different. The vertical structure of the longshore and cross-shore currents is shown in Fig. 2. Both models produce the classical undertow profile (e.g. Svendsen 2006, chapter 12) inside the surf zone (x > 700 m) with strong return flow in the lower part of the water column and weaker flow in the upper part of the water column. Outside the surf zone (x < 600 m), SC is producing undertow with fairly depth uniform or a slightly increased flow near the surface in accordance with Putrevu and Svendsen (1993), whereas,ROMSis producing undertow which is still stronger in the lower part of the water column, albeit with much less curvature than inside the surf zone. Both models predict longshore current profiles inside the surf zone which are stronger near the surface than

near the bottom, although with less curvature than for the undertow as expected. The curvature for the results from ROMS is a bit larger than the results from SC.